| |
| | |
|
Figure 1:
Three legged intersection
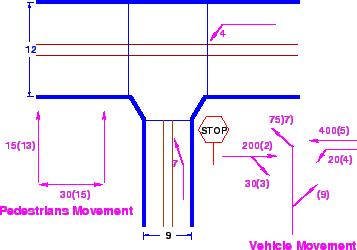 |
For a three legged intersection given in figure 1
determine the control delay and level of service for movement 7.
The total volume of both pedestrian and vehicular traffic at each movement is
given in the figure itself.
Following data is also given:
- The speed of the pedestrians is 1.2m/s
- All flows contains 10% trucks
- The percentage of the grade is 0.00
- Ignore moments coming from south bound
- The analysis period is 15 min. (T=0.25)
- Compute the critical gap and follow up time:
- Critical gap
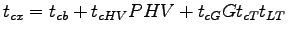 .
From table. .
From table. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) and
table. and
table. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) we have we have
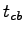 = 7.1 s , = 7.1 s , 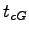 = 0.2, = 0.2, 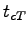 = 0.0, = 0.0, 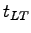 = 0.0.
Then = 0.0.
Then 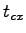 at movement 7 computed as: at movement 7 computed as:
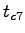 = 7.1 + 1.0 = 7.1 + 1.0 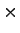 0.1+0.2 0.1+0.2 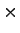 0.0 - 0.0 - 0.0 = 6.50 sec 0.0 - 0.0 - 0.0 = 6.50 sec
- To compute the Follow up time:
From table.
![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) and
table. and
table. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) we have we have
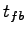 = 3.5 s , = 3.5 s , 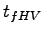 = 0.9.
Then = 0.9.
Then 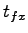 at movement 7 computed as: at movement 7 computed as:
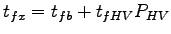 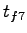 = 3.5 + 0.9 = 3.5 + 0.9  0.1 = 3.59 sec. 0.1 = 3.59 sec.
- Compute the conflicting flow rate:
- Determining potential capacity:
- Determine the impudence effect of the movement capacity for movement 7:
From the given figure movement 7 is impeded by vehicular movement 4 and 1 and
pedestrian 13 and 15.
- Pedestrian impedance probability computed as:
- Vehicular impedance probabilities are:
- Once the pedestrian and vehicular impedance is determined, the moment
capacity is computed as:
- Delay computation:
The delay is Calculated by using the formula
The delay of movement 7 is 18.213 sec/veh.
- Determine the level of service:
From the computed delay (18.213 se) in step 5 the level of service is
LOS C obtained from HCM table.
|
|
| | |
|
|
|