|
Capacity is defined as the maximum number of vehicles, passengers, or the like,
per unit time, which can be accommodated under given conditions with a
reasonable expectation of occurrence.
Potential capacity describes the capacity of a minor stream under ideal
conditions assuming that it is unimpeded by other movements and has exclusive
use of a separate lane.
Once of the conflicting volume, critical gap and follow up time are known
for a given movement its potential capacity can be estimated using gap
acceptance models.
The concept of potential capacity assumes that all available gaps are used by
the subject movement i.e.; there are no higher priority vehicular or pedestrian
movements and waiting to use some of the gaps it also assumes that each movement
operates out of an exclusive lane.
The potential capacity of can be computed using the formula:
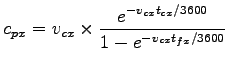 |
(1) |
where,
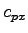 is the potential capacity of minor movement is the potential capacity of minor movement 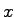 (veh/h), (veh/h),
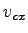 is the conflicting flow rate for movement is the conflicting flow rate for movement 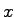 (veh/h), (veh/h),
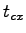 is the critical gap for minor movement is the critical gap for minor movement 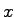 , and , and
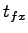 is the follow-up time movement is the follow-up time movement 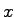 .
Vehicles use gaps at a TWSC intersection in a prioritized manner.
When traffic becomes congested in a high-priority movement, it can impede
lower-priority movements that are streams of Ranks 3 and 4 as shown in
Fig. .
Vehicles use gaps at a TWSC intersection in a prioritized manner.
When traffic becomes congested in a high-priority movement, it can impede
lower-priority movements that are streams of Ranks 3 and 4 as shown in
Fig. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) from using gaps in the traffic stream, reducing
the potential capacity of these movements.
The ideal potential capacities must be adjusted to reflect the impedance effects
of higher priority movements that may utilize some of the gaps sought by lower
priority movements.
This impedance may come due to both pedestrians and vehicular sources called
movement capacity. from using gaps in the traffic stream, reducing
the potential capacity of these movements.
The ideal potential capacities must be adjusted to reflect the impedance effects
of higher priority movements that may utilize some of the gaps sought by lower
priority movements.
This impedance may come due to both pedestrians and vehicular sources called
movement capacity.
The movement capacity is found by multiplying the potential capacity by an
adjustment factor.
The adjustment factor is the product of the probability that each impeding
movement will be blocking a subject vehicle.
That is
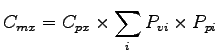 |
(2) |
where,
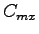 is the movement capacity in vph, is the movement capacity in vph,
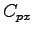 is the potential capacity movement x in vph, is the potential capacity movement x in vph,
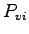 is the probability that impeding vehicular movement is the probability that impeding vehicular movement 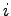 is not blocking
the subject flow; (also referred to as the vehicular impedance factor for
movement is not blocking
the subject flow; (also referred to as the vehicular impedance factor for
movement 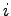 , ,
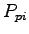 is the probability that impeding pedestrian movement is the probability that impeding pedestrian movement 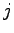 is not blocking
the subject flow; also referred to us the pedestrian impedance factor for the
movement is not blocking
the subject flow; also referred to us the pedestrian impedance factor for the
movement 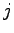 .
Priority 2 vehicular movements LTs from major street and RTs from minor street
are not impeded by any other vehicular flow, as they represent the highest
priority movements seeking gaps.
They are impeded, however, by Rank 1 pedestrian movements.
Priority 3 vehicular movements are impeded by Priority 2 vehicular movements and
Priority l and 2 pedestrian movements seeking to use the same gaps.
Priority 4 vehicular movements are impeded by Priority 2 and 3 vehicular
movements, and Priority 1 and 2 pedestrian movements using the same gaps.
Table. 1 lists the impeding flows for each subject
movement in a four leg.
Generally the rule stated the probability that impeding vehicular movement .
Priority 2 vehicular movements LTs from major street and RTs from minor street
are not impeded by any other vehicular flow, as they represent the highest
priority movements seeking gaps.
They are impeded, however, by Rank 1 pedestrian movements.
Priority 3 vehicular movements are impeded by Priority 2 vehicular movements and
Priority l and 2 pedestrian movements seeking to use the same gaps.
Priority 4 vehicular movements are impeded by Priority 2 and 3 vehicular
movements, and Priority 1 and 2 pedestrian movements using the same gaps.
Table. 1 lists the impeding flows for each subject
movement in a four leg.
Generally the rule stated the probability that impeding vehicular movement
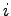 is not blocking the subject movement is computed as is not blocking the subject movement is computed as
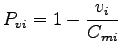 |
(3) |
where,
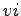 is the demand flow for impeding movement is the demand flow for impeding movement 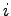 , and , and
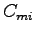 is the movement capacity for impeding movement is the movement capacity for impeding movement 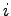 vph.
Pedestrian impedance factors are computed as:
One of the impeding effects for all the movement is pedestrians movement.
Both approaches of Minor-street vehicle streams must yield to pedestrian
streams.
Table. 1 shows that relative hierarchy between
pedestrian and vehicular streams used.
A factor accounting for pedestrian blockage is computed by
Eqn. 4 on the basis of pedestrian volume, the pedestrian
walking speed, and the lane width that is: vph.
Pedestrian impedance factors are computed as:
One of the impeding effects for all the movement is pedestrians movement.
Both approaches of Minor-street vehicle streams must yield to pedestrian
streams.
Table. 1 shows that relative hierarchy between
pedestrian and vehicular streams used.
A factor accounting for pedestrian blockage is computed by
Eqn. 4 on the basis of pedestrian volume, the pedestrian
walking speed, and the lane width that is:
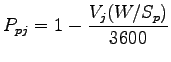 |
(4) |
where,
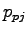 is the pedestrian impedance factor for impeding pedestrian movement is the pedestrian impedance factor for impeding pedestrian movement 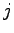 , ,
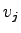 is the pedestrian flow rate, impeding movement is the pedestrian flow rate, impeding movement 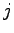 in peds/hr, in peds/hr,
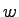 is the lane width in m, and is the lane width in m, and
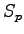 is the pedestrian walking speed in m/s. is the pedestrian walking speed in m/s.
Table 1:
Relative pedestrian/vehicle hierarchy
| Vehicle Stream |
Must Yield to |
Impedance Factor for |
| |
Pedestrian Stream |
Pedestrians, 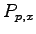 |
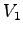 |
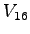 |
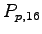 |
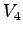 |
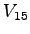 |
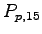 |
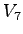 |
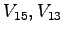 |
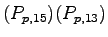 |
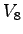 |
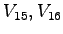 |
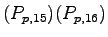 |
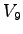 |
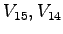 |
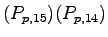 |
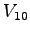 |
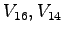 |
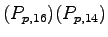 |
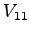 |
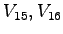 |
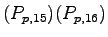 |
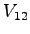 |
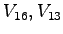 |
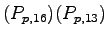 |
The capacities of individual streams (left turn, through and right turn) are
calculated separately.
If the streams share a common traffic lane, the capacity of the shared lane is
then calculated according to the shared lane procedure.
But movement capacities still represent an assumption that each minor street
movement operates out of an exclusive lane.
Where two or three movements share a lane its combined capacity computed as:
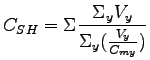 |
(5) |
where,
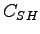 is the shared lane capacity in veh/hr, is the shared lane capacity in veh/hr,
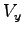 is the flow rate, movement is the flow rate, movement 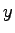 sharing lane with other minor street flow, and sharing lane with other minor street flow, and
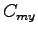 is the movement capacity of movement is the movement capacity of movement 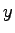 sharing lane with other minor
street. sharing lane with other minor
street.
|
|