Solids of Revolution
We first consider solids of revolution ( 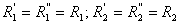 ) for which the contact area is circular with radius ) for which the contact area is circular with radius 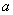 . The boundary condition for displacement within the contact area is given by . The boundary condition for displacement within the contact area is given by
where 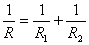 is the relative curvature. A distribution of pressure which gives the displacement of the form 8.16 is is the relative curvature. A distribution of pressure which gives the displacement of the form 8.16 is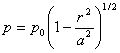 for which the normal displacement has been obtained as for which the normal displacement has been obtained as
Since pressure acting on either body is equal, we add the expressions for displacements on the body 1 and 2
|
and 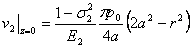 |
(8.18) |
Furthermore we define an equivalent elastic modulus 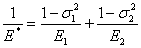 and add the normal displacements, to deduce an expression very similar to 8.16. and add the normal displacements, to deduce an expression very similar to 8.16.
The expressions for 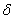 and and 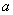 is now readily obtained as, is now readily obtained as,
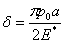 , |
|
(8.20) |
Since in most practical situations we have the data of total load compressing the solids, we obtain it as in equation 5.21:
Then we can obtain the expressions for 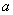 , , 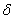 and and 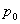 : :
|