Herttzian Mechanics (contd...)
Let's say two cylinders are in contact, so that the load per unit of the axial length is 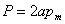 , which results in, , which results in,
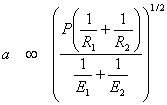 and 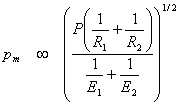 |
(8.14) |
i.e. both contact pressure and the contact width both increase with the square root of the applied load.
Let's say we are now dealing with solids of revolution so that the contact area is a circle of radius, then  , ,
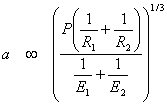 and 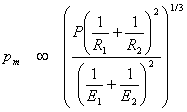 |
(8.15) |
In this case, the radius of contact circle and contact pressure increases with the cube root of the load.
While in last paragraph we deduced the relation of contact width to applied load by dimensional analysis, now we will do that in a more rigorous manner by solving the elasticity equations.
|