An estimate of the critical stress that ensues the wrinkling phenomenon can be obtained by dividing the critical load by the cross-sectional area of the film:
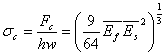 |
(31.7) |
Then the critical strain is written as,
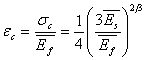 |
(31.8) |
Notice that critical strain is a function only of ratio of the moduli of substrate and the film and remains independent of the thickness. The significance of the critical strain is that beyond it a wrinkling wavelength is established; with further increase in the strain, the amplitude of the wrinkling increases which accommodates the excess strain while the wavelength remains nearly constant. By assuming that wavelength of instability remains independent of the excess strain, an estimate of it, can be obtained by analysing the geometry of the wrinkles,
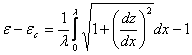 |
(31.9) |
Notice, the quantity within the integral sign defines the contour length of the wrinkle over one wavelength. Substituting 31.3 into 31.9 and noting that 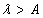 , so that, , so that,
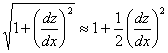 |
(31.10) |
Noting that, 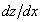 is very small, we deduce, is very small, we deduce,
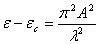 , , 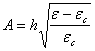 |
(31.11) |
Equations 31.6, 31.8 and 31.11 capture the essential features of the wrinkling instability, the wavelength, the critical strain at which the instability ensues and the growth of amplitude of the instability with the applied strain.
|