Surface wrinkling can be analysed by considering the classical force balance equation for bending of a stiff film on a compliant elastic substrate.
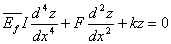 |
(31.2) |
Where, 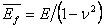 is the plane strain modulus and is the plane strain modulus and 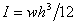 is the moment of inertia of the stiff film. is the moment of inertia of the stiff film. 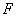 is the uni-axially applied load. The constant is the uni-axially applied load. The constant 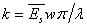 , is called the Winkler’s modulus of an elastic half-space. The subscripts , is called the Winkler’s modulus of an elastic half-space. The subscripts 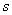 and and 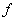 denote the substrate and the film respectively. Notice the second term represents the external compressive load which causes the buckling instability, the first term represents the bending force in film which suppresses the perturbations with short wavelength, the third term defines the force due to deformation normal to the surface of the film, it suppresses large wavelength fluctuations. We assume that the perturbation in vertical deflection of the film can be represented by the following sinusoidal function denote the substrate and the film respectively. Notice the second term represents the external compressive load which causes the buckling instability, the first term represents the bending force in film which suppresses the perturbations with short wavelength, the third term defines the force due to deformation normal to the surface of the film, it suppresses large wavelength fluctuations. We assume that the perturbation in vertical deflection of the film can be represented by the following sinusoidal function
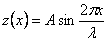 |
(31.3) |
Which when substituted in equation 31.2 results in following expanded form in terms of 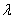
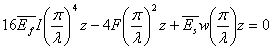 |
(31.4) |
Solving for the applied force 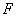 , we obtain, , we obtain,
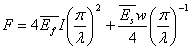 |
(31.5) |
The minimum force that can cause the instability can be found by putting, 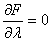 , which yields the following relation for wavelength, , which yields the following relation for wavelength,
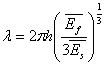 |
(31.6) |
|