Finally we obtain the following characteristic equation,
We can consider the asymptotic situation of 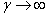 , implying that thickness of the slab increases to a half space, at this situation, the characteristic equation reduces to , implying that thickness of the slab increases to a half space, at this situation, the characteristic equation reduces to
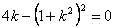 or 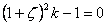 |
(30.12) |
Notice that equation 30.12 coincides with 29.22, implying that for very short slab the buckling deformation of the slab degenerates to surface instability.
The other extreme is the limit of very slender slab for which, 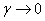 , for which we can simplify the characteristic equation by using , for which we can simplify the characteristic equation by using
in which we have neglected higher order terms. Substitution of these expressions into 30.11 results in,
Notice that if we simplify the above equation to the first order it yields
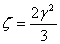 or 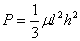 |
(30.15 |
It can be shown that this expression matches with that is derived for Euler buckling instability for thin plates. For example, from lecture 14, under small bending approximation, the transverse deflection 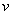 of a thin plate of thickness of a thin plate of thickness 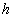 , under axial load , under axial load 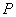 is written as, is written as,
For an incompressible material, 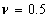 , the above equation simplifies to, , the above equation simplifies to,
If the deflection is assumed to be sinusoidal, 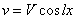 , the buckling load is deduced as, , the buckling load is deduced as,
This relation for buckling load matches with deduced earlier in equation 30.15
|