The extension ratio 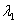 ( (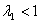 ) is a measure of the compressive strain along ) is a measure of the compressive strain along 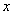 , then the length and thickness of the slab in the compressed state respectively are: , then the length and thickness of the slab in the compressed state respectively are:
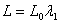 , 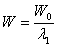 |
(30.3) |
We can consider also a situation that the slab freely deform perpendicular to the  plane, so that plane, so that
And the initial compressive stress and the incremental modulus are related as
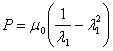 and 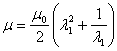 |
(30.5) |
The length and width of the compressed slab are then written as
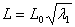 , 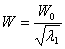 |
(30.6) |
Let us now say that the initial stressed condition of the elastic block is now perturbed by applying incremental deformation in plane strain that is parallel to the 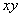 plane. The equations for incremental deformations are then same as that presented earlier, i.e. equations 29.14 to 29.18: plane. The equations for incremental deformations are then same as that presented earlier, i.e. equations 29.14 to 29.18:
The solution of these equations, which will correspond to the buckling of the block, can be written as,
In which, 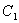 and and 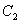 are constants. We have as before, are constants. We have as before,
The boundary conditions at the free surface of the slab is written as
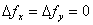 at 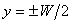 |
(30.9) |
The expressions for  and and 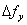 are written directly from the previous section, i.e. equation 29.22 Substitution of the expressions for are written directly from the previous section, i.e. equation 29.22 Substitution of the expressions for 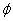 and and 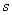 from 30.7 into 30.9 yields, from 30.7 into 30.9 yields,
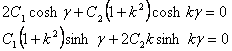 t |
(30.10) |
Where, 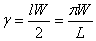
|