Resolution of any stress system into uniform tension and shearing stress:
Note that the quantity 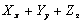 is invariant with respect to transformations from one set of rectangular axes to another, so that we can call the quantity is invariant with respect to transformations from one set of rectangular axes to another, so that we can call the quantity 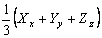 the “mean tension at a point”. the “mean tension at a point”.
For a stress system with uniform normal pressure 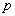 , this quantity is , this quantity is 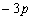 . Using this concept we can resolve any stress system into components characterized by the existence and non-existence of mean tension, e.g. . Using this concept we can resolve any stress system into components characterized by the existence and non-existence of mean tension, e.g.
The stress system 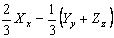 involves no mean-tension, furthermore, we can choose co-ordinates involves no mean-tension, furthermore, we can choose co-ordinates 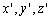 such that the normal tractions corresponding to these axes vanish. such that the normal tractions corresponding to these axes vanish.
In a word, this stress system involves no mean tension. Hence, we can say that any stress system at a point is equivalent to uniform tension in all directions and tangential traction across three planes which cut each other at right angles.
Consider a body of an arbitrary shape is subjected to a constant pressure p which remains constant in all directions, such that,
and the state of strain in the body is such that,
The quantity 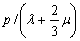 is a measure of its cubicle compression and the quantity, is a measure of its cubicle compression and the quantity, 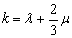 is called the modulus of compression. It is obtained by dividing the mean tension is called the modulus of compression. It is obtained by dividing the mean tension 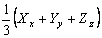 at a point by cubicle dilation at that point. at a point by cubicle dilation at that point.
|