Resolution of any stress system into uniform tension and shearing stress (contd...)
A cylinder or prism of any form, subjected to tension 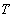 which is uniform over its plane ends and free from traction at the lateral surfaces. Then we can write, which is uniform over its plane ends and free from traction at the lateral surfaces. Then we can write,
Then from equation 3.15, state of strain can be written as,
where, we put,
The quantity 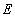 obtained by dividing the simple longitudinal tension by the measure of the extension produced by it, is known as the Young's modulus . The number obtained by dividing the simple longitudinal tension by the measure of the extension produced by it, is known as the Young's modulus . The number 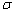 is the ratio of lateral contraction to longitudinal extension is called Poisson's ratio . is the ratio of lateral contraction to longitudinal extension is called Poisson's ratio . 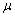 is called shear modulus. is called shear modulus.
Furthermore, note the relations:
Material |
Specific
garvity,
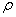
|
Young’s
modulus,
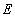
|
Bulk
modulus,
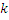
|
Shear
modulus,
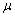
|
Poisson’s
ratio,
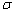
|
| |
|
N/m 2 |
N/m 2 |
N/m 2 |
|
Steel |
7.849 |
2.1x10 12 |
1.84x10 12 |
8.2x10 11 |
0.31 |
Brass |
8.471 |
1.085x10 12 |
1.05x10 12 |
3.66x10 11 |
0.327 |
Copper |
8.843 |
1.234x10 12 |
1.684x10 12 |
|
0.378 |
Glass |
2.942 |
6.03x10 11 |
4.15x10 11 |
2.4x10 11 |
0.258 |
|