| |
Consider an initial stress field
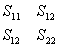 |
(26.2) |
If the plane continuum is deformed, any point P is displaced to a point P' of co-ordinates x, h and the stress at that point P' acquires a new value defined by the components
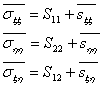 |
(26.3) |
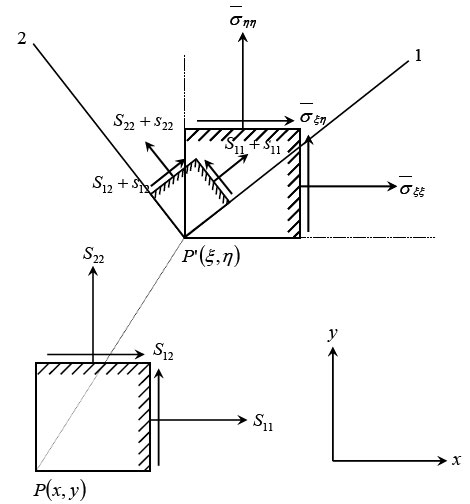
Figure 26.2
These components are referred to the fixed directions 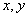 . The components . The components 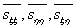 represent the increment of the total stress at the displaced point represent the increment of the total stress at the displaced point 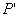 of co-ordinates of co-ordinates 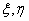 after deformation. Now let’s introduce the idea that the incremental components are not only due to the strain but also to the fact that the initial stress field has been rotated by a certain angle when moving from after deformation. Now let’s introduce the idea that the incremental components are not only due to the strain but also to the fact that the initial stress field has been rotated by a certain angle when moving from 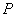 to to 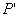 . In other words, if there is only translation followed by a solid body rotation there will be incremental stress components . In other words, if there is only translation followed by a solid body rotation there will be incremental stress components 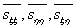 due to this rotation, this is of geometric origin. In addition, if the material undergoes a strain, there will be an incremental stress of purely physical origin. Hence it is needed to separate the geometry from the physics in expressing the incremental stress components. This can be done, if we in stead of referring them to the original directions due to this rotation, this is of geometric origin. In addition, if the material undergoes a strain, there will be an incremental stress of purely physical origin. Hence it is needed to separate the geometry from the physics in expressing the incremental stress components. This can be done, if we in stead of referring them to the original directions 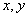 , we refer to a new direction , we refer to a new direction 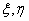 . These new directions are rotated with respect to the original direction by angle . These new directions are rotated with respect to the original direction by angle 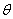 which is equal to the local rotation of the material. Its approximate value to the first order is, which is equal to the local rotation of the material. Its approximate value to the first order is,
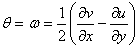 |
(26.4) |
|