For the balloon inflation problem, this relation simplifies to
Then the differential strain energy:
And the mechanical energy done to expand the volume:
Balancing these two one obtains,
Then the condition for obtaining the two extremes translate to,  , or, , or,
Thus neo-Hookean relation alone is not sufficient for the inflation of the balloon, we need a two parameter model like the Mooney-Rivlin equation to account for it.
The Mooney–Rivlin form agrees well with the experiment at small strains. However at modest strain beyond 10% the second term of the equation 12.61 looses importance, therefore there is a need for modifying this equation. This is done by replacing it by a logarithmic term as follows:
For soft rubbers the constants  and and 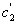 are found to be 0.25-0.5 MPa. are found to be 0.25-0.5 MPa.
Many materials like rubber strain hardens at large strain which is not captured by the above equations. The strain hardening behaviour of rubber is accounted for further modification of equation (25.11) in which the maximum possible value of measured quantity 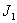 is represented as is represented as 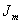 : :
Calculations from 25.1 to 25.5 can now be repeated.
|