Balancing these energies, we have,
This is the expression for pressure for a neo = Hookean balloon. It is easy to see that pressure required to inflate the balloon is zero at 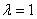 and also at and also at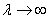 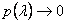 . Then there should be a maxima, which can be obtained by putting . Then there should be a maxima, which can be obtained by putting
which yields 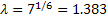 , The maximum pressure is then calculated as , The maximum pressure is then calculated as
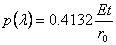 . The maximum pressure depends upon the ratio . The maximum pressure depends upon the ratio 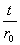 and also on the Young’s modulus and also on the Young’s modulus 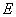 , but the stretch at which the pressure becomes maximum remains constant and is equal to , but the stretch at which the pressure becomes maximum remains constant and is equal to 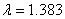 . Pressure decreases to zero asymptotically. However, . Pressure decreases to zero asymptotically. However,
in experiments we do not see that. The pressure goes through a maxima, then a minima after which it increases again. The Hookean strain energy function can not capture this complex behavior of the pressure vs extension ratio. In order to explain it we need more involved relation, one such strain energy function is proposed by Mooney and Rivlin and is known as Mooney-Rivlin equation which can be written as,
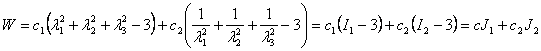 |
(25.6) |
Here  and and 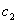 are constants signifying material properties such that are constants signifying material properties such that 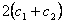 equates the shear modulus equates the shear modulus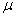 . Notice that the principal extension ratios are actually obtained as the eigen values of the matrix 8.1, so that the quantities . Notice that the principal extension ratios are actually obtained as the eigen values of the matrix 8.1, so that the quantities 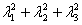 , , 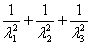 and and 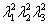 are invariant. We can expand equation (25.6) as a power series in terms of are invariant. We can expand equation (25.6) as a power series in terms of 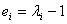 which includes the terms for which includes the terms for 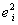 and and 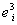 , as a result, the Mooney–Rivlin form of strain energy gives good agreement with experiment at small strains. The Neo-Hookean material is a subset of the Mooney-Rivlin material. , as a result, the Mooney–Rivlin form of strain energy gives good agreement with experiment at small strains. The Neo-Hookean material is a subset of the Mooney-Rivlin material.
|