Notice that for the solenoidal portion of the rod, the vertical distance traveled by the dead weight is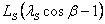 and is not and is not 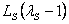 . For the straight portion, however, the distance traveled by the dead weight remains . For the straight portion, however, the distance traveled by the dead weight remains 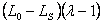 . .
Similarly, the energy spent by the external torque 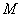 in twisting the rod is obtained as, in twisting the rod is obtained as,
Notice that the total angle turned by the end moment is given as: 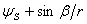
Then the total energy of the system and that of the external load and torque are written as
Minimizing the total energy with respect to 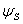 yields yields
Minimizing the total energy with respect to 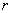 yields yields
Similarly minimizing the total energy with respect to 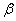 yields yields
 |
(24.17) |
Substitution of expression for 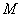 in equation 24.14 into 24.15 and solution of equations 24.15 and 24.16, for in equation 24.14 into 24.15 and solution of equations 24.15 and 24.16, for 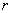 and and 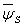 yields yields
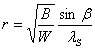 ,  |
(24.18) |
Equation 24.15 to 24.18 present us six equations for eight unknowns: 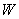 , , 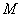 , , 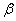 , , 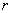 , , 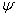 , , 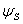 , , 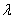 and and 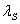 . The ideas here is to fix the values for, say . The ideas here is to fix the values for, say 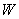 and and 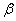 , and calculate the values for six other unknowns. , and calculate the values for six other unknowns.
The threshold values of different parameters at which the straight rod would turn to a helix is obtained by considering the stability of the above solutions. The solutions are stable when the eigen values of the Hessian matrix written as 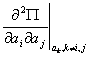 with with 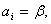 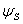 and and 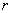 remain positive. remain positive.
|