Let us now consider that the cylindrical rod of length 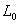 under the action of both extension and torsion does not remain straight but undergoes spontaneous transformation to solenoidal helices characterized by the helix radius under the action of both extension and torsion does not remain straight but undergoes spontaneous transformation to solenoidal helices characterized by the helix radius 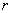 and helix angle and helix angle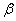 . Question arises at which threshold twist density this transformation occurs? . Question arises at which threshold twist density this transformation occurs?
The threshold condition can be obtained by carrying out the minimization of the total energy of the system. Let us consider that the contour length of the undeformed rod that goes to form the helix is 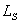 within which the extension ratio is within which the extension ratio is 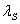 . The twist density . The twist density 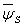 of the rod in the solenoidal portion comprises of two components: that due to actual internal torsion of the rod and that due to kinematic torsion associated with bending of the rod: of the rod in the solenoidal portion comprises of two components: that due to actual internal torsion of the rod and that due to kinematic torsion associated with bending of the rod: 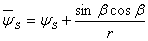 . In addition to torsion, the solenoid is also characterized by the total curvature given as . In addition to torsion, the solenoid is also characterized by the total curvature given as 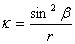 . .
Combining the extensional energy of the rod in its straight and solenoidal portion, the total extensional energy is written as:
Similarly, the total torsional energy is obtained as,
The bending energy of the deformed rod is written as 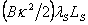 , where , where 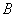 , bending rigidity is defined as , bending rigidity is defined as 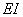 . Here . Here 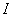 is the moment of inertia of the deformed rod, writes as, is the moment of inertia of the deformed rod, writes as, 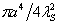 . Then the bending energy of the rod is obtained as . Then the bending energy of the rod is obtained as
The energy spent by the dead weight 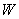 in extending is obtained by multiplying the dead weight with the net vertical distance traveled, in extending is obtained by multiplying the dead weight with the net vertical distance traveled,
|