Stability of Equilibrium
Let us consider a cube of an incompressible, neo-Hookean material with unit edges in the unstrained state. It is strained to dimensions 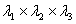 under the action of three forces under the action of three forces 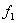 , , 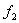 and and 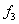 so that the strain energy stored in it can be written as, so that the strain energy stored in it can be written as,
and the work done by these forces is
The net energy can be expressed as the summation of the above two:
The equilibrium of forces for all possible values of 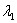 , , 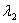 and and 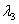 can be obtained by finding the minima of the above total energy, such that the following conditions are satisfied: can be obtained by finding the minima of the above total energy, such that the following conditions are satisfied:
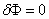 and and 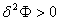 |
(23.8) |
Writing 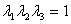 we can obtain the allowable variations we can obtain the allowable variations 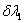 , , 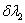 and and 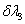 of of 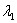 , , 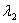 and and 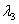 respectively, which are to satisfy the following condition: respectively, which are to satisfy the following condition:
Then 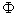 can be rewritten as a function of can be rewritten as a function of 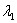 and and 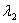 : :
Then the quantities 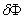 and and 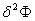 can be written as, can be written as,
|