| |
Now consider the following situation in which a cube is extended along the three axes so that we have the following extension ratios:
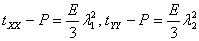 and and 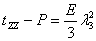 |
(23.4) |
What can we say about the uniqueness of the pressure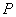 , or, can it be uniquely defined? Let us say, for simplicity that , or, can it be uniquely defined? Let us say, for simplicity that 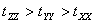 . The we can think about the following two equations, at their intersections lie the solution of . The we can think about the following two equations, at their intersections lie the solution of 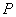 . .
Needless to say that 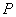 will intersect will intersect  at at 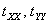 and and 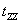 . Furthermore, when, . Furthermore, when, 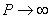 , , 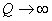 and when and when 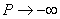 , , 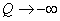 . Hence, the . Hence, the 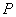 curve look like the one plotted in figure. curve look like the one plotted in figure.
Since 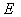 is positive, the is positive, the 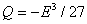 line will lie beneath the line will lie beneath the 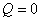 line, so that curve intersect line, so that curve intersect 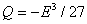 either at one location or at three locations either at one location or at three locations 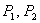 and and 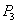 . The figure shows that one of the solutions, for example . The figure shows that one of the solutions, for example 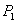 should be less than should be less than 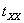 , whereas, other two solutions , whereas, other two solutions 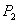 and and 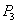 should be between should be between 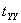 and and 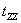 . Then from equation (23.4) . Then from equation (23.4)
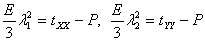 and and 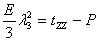 |
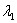 is real and is real and 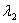 and and 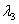 are complex numbers. Therefore, it is obvious that there is only solution possible for are complex numbers. Therefore, it is obvious that there is only solution possible for 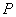 . .
|