The stored energy function
Consider a cubic element having unit edges is strained in such a way that in deformed state it is a cuboid having edges parallel to the axes of strain ellipsoid with lengths 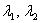 and and 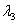 respectively. Then due to incompressibility, respectively. Then due to incompressibility,
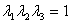 |
(22.14) |
Then the work done in straining the material quasi-statically is 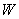 which can be worked out by considering the stresses which act on the deformed element which can be worked out by considering the stresses which act on the deformed element 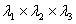 . .
The element is subjected to three mutually perpendicular forces 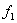 , , 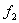 and and 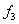 which are given by which are given by 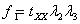 , , 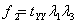 and and 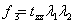 ,. Here ,. Here  , , 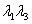 and and 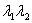 are the areas on which the stresses are the areas on which the stresses 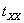 , , 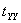 and and 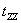 act. Using the expression for act. Using the expression for 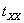 , , 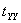 , , 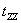 and the incompressibility relation we have, and the incompressibility relation we have,
Work done in straining an element of volume 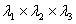 to to 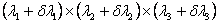 is is
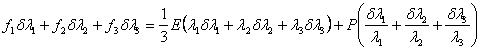 |
(22.17) |
Hence the work done in straining the material quasi-statically from dimension 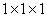 to to 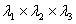 is is
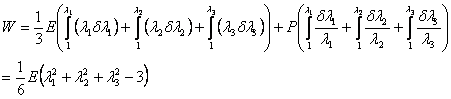 |
(22.18) |
For an ideal rubber like material the elastic modulus 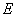 is given as is given as 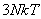 where where 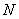 is the number of segments per unit volume, is the number of segments per unit volume, 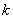 is the Boltzmann’s constant and is the Boltzmann’s constant and 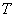 is the absolute temperature. is the absolute temperature.
|