For a pure homogeneous deformation, suppose that 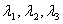 are the lengths in the deformed state of linear elements parallel to the axes are the lengths in the deformed state of linear elements parallel to the axes 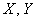 and and 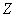 respectively which have unit lengths in the undeformed state. Then by making respectively which have unit lengths in the undeformed state. Then by making 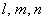 successively successively 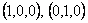 and and 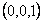 , we see that , we see that
Simple extension:
Consider the simple extension along x axis of a, incompressible neo-Hookean material for whom the stress-strain relations take the form:
Since 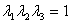 , we have , we have 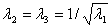 and and 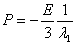 which gives, which gives,
Simple shear:
Thus shearing stresses alone can not maintain a state of simple shear in the material. If the stresses 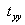 and and 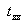 are zero, then the stresses are zero, then the stresses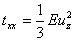 ; and if ; and if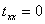 , then , then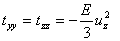 . Thus two possible stress systems which can maintain a simple shear: . Thus two possible stress systems which can maintain a simple shear:
(i) A shearing stress 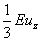 in the in the 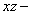 plane together with a normal stress plane together with a normal stress 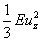 parallel to the parallel to the 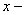 axis. axis.
(ii) A shearing stress 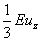 in the in the 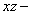 plane together with two normal stresses of magnitude plane together with two normal stresses of magnitude 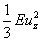 parallel to the parallel to the 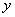 and and 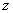 axes. axes.
|