For a thin film ( 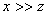 ), we may use the lubrication approximation so that the equations of equilibrium 20.1 simplify to ), we may use the lubrication approximation so that the equations of equilibrium 20.1 simplify to
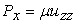 |
(20.9) |
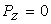 |
Physically, this simplification results from the dominant balance between shear stress and the horizontal pressure gradients in these thin layers. Equation 20.9 signifies that the pressure in the film is constant along the thickness coordinate, so that we can equate 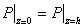 , which on integration yields , which on integration yields
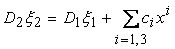 |
(20.10) |
The integration constants 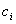 are equal to zero since the displacements are equal to zero since the displacements 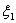 and and 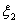 of the plates must vanish at of the plates must vanish at 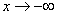 , yielding , yielding
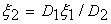 |
(20.11) |
Integrating equations 20.9 in the region 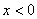 and using the boundary conditions 11.21, yields and using the boundary conditions 11.21, yields
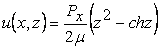 |
(20.12) |
Here, the constant c = 1 for the case of perfect adhesion ( Case I) and c =2 for the case of perfect slippage ( Case II ) . Substituting this result into 20.2 and integrating the equation across the thickness of the film and using the boundary conditions 20.3, 20.6 and 20.7 yields an equation for the vertical displacement of the interface of the elastomeric film in the region 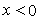 where it is attached to the flexible plate where it is attached to the flexible plate
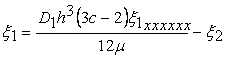 |
(20.13) |
Substituting the expression for 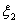 from equation 11.29 in equation 11.31, we obtain, from equation 11.29 in equation 11.31, we obtain,
 |
(20.14) |
Notice that the expression in equation 20.14 matches with that of equation 19.7 derived for the experiment in which a single flexible plate is peeled of a layer of elastic adhesive bonded to a rigid substrate. Here, however, we obtain the definition of an equivalent flexural rigidity 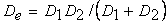 , i.e. the harmonic mean of the rigidities of the two flexible plates which implies that the experiment with two flexible plates is equivalent to one with a single plate having an equivalent flexural rigidity. , i.e. the harmonic mean of the rigidities of the two flexible plates which implies that the experiment with two flexible plates is equivalent to one with a single plate having an equivalent flexural rigidity.
|