In order to determine the work of adhesion by this experiment, we analyze the contact mechanics of this coupled elastic system. Assuming that the adhesive layer is incompressible, linearly elastic and is loaded in the plane strain, the 2-dimensional stress equilibrium equations are
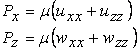 |
(20.1) |
Here 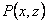 is the pressure in the elastic layer, is the pressure in the elastic layer, 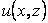 and and 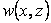 are the components of displacement field in the are the components of displacement field in the 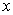 and and 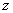 directions (figure 1) and directions (figure 1) and 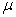 is the shear modulus of the layer. The incompressibility relation is written as, is the shear modulus of the layer. The incompressibility relation is written as,
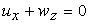 |
(20.2) |
We solve equation 20.1 and 20.2 by using the following boundary conditions:
(a) We assume perfect bonding at the interface of the adhesive film and the underlying flexible plate (2), so that boundary conditions at this interface are:
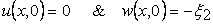 |
(20.3) |
Here,  denotes the vertical deflection of the flexible plate (2). denotes the vertical deflection of the flexible plate (2).
(b) Continuity of the normal stress across the interface of the film and the contacting plate (2) i.e. at 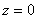 results in the boundary condition: results in the boundary condition:
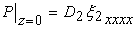 |
(20.4) |
(c) At the interface of the film and the flexible plate (1) we have a more complicated situation since the flexible plate is in contact with the film only over part of the domain. In the region 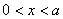 , there is no traction either on the plate or on the film so that the boundary conditions read , there is no traction either on the plate or on the film so that the boundary conditions read
Here 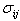 denote the components of the two-dimensional stress tensor (and not derivatives), and. denote the components of the two-dimensional stress tensor (and not derivatives), and.
(d) In the region 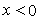 , the film remains in contact with the plate (1), so that the vertical displacement of the film and that of the flexible plate at this interface are equal, which results in, , the film remains in contact with the plate (1), so that the vertical displacement of the film and that of the flexible plate at this interface are equal, which results in,
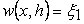 |
(20.6) |
(e) Furthermore, continuity of the normal stress across this interface i.e. at 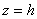 yields the boundary condition yields the boundary condition
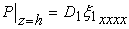 |
(20.7) |
(f) For the tangential traction, we can consider the following generalized boundary condition:
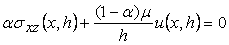 |
(20.8) |
where 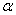 is a parameters characterizing the nature of the bonding at the interface of the film and the cover plate When is a parameters characterizing the nature of the bonding at the interface of the film and the cover plate When 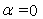 , , 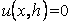 corresponding to a perfect adhesion at the said interface (Case I), corresponding to a perfect adhesion at the said interface (Case I), 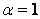 implies that implies that 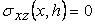 and corresponds to the case of perfect slippage at the interface (Case II). In general and corresponds to the case of perfect slippage at the interface (Case II). In general 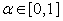 . .
|