Simplifications (Contd...)
Consider the equilibrium of a tetrahedral portion of the body which has three edges along the three axes of the co-ordinate and the vertex at which they meet at the origin O. Say 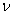 is the direction normal to the plane ABC drawn away from the interior of the plane. Then the direction cosines of this plane are is the direction normal to the plane ABC drawn away from the interior of the plane. Then the direction cosines of this plane are 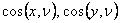 and and 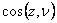 . Let's say that the plane is at a distance . Let's say that the plane is at a distance 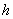 from origin O with from origin O with 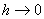 . If . If  is the area of this plane then the areas of the remaining faces are is the area of this plane then the areas of the remaining faces are 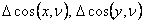 and and 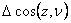 respectively. respectively.
When the tetrahedron is small, the traction across the face 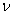 be be 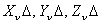 and those on the remaining faces to be and those on the remaining faces to be 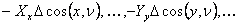 and and 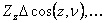 . .
by this equation we express traction across any plan through O in terms of the traction across planes parallel to the coordinate planes.
Now, consider a very small cube with edges parallel to the coordinate axes. The value 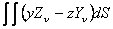 for the cube can be taken as for the cube can be taken as 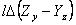 , where , where 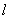 is the length of any edge. Hence from the results of the last paragraph, we have, is the length of any edge. Hence from the results of the last paragraph, we have,
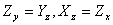 and and 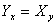 . Thus, the number of components that must be specified in order that the stress at a point may be specified is six, three normal components and three tangential tractions. . Thus, the number of components that must be specified in order that the stress at a point may be specified is six, three normal components and three tangential tractions.
|