Simplifications
At equilibrium the accelerations 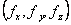 are zero. are zero.
Secondly, the volume of integration is very small in all its dimensions and 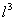 be the volume, then both sides of eqn 2.5 in the limit be the volume, then both sides of eqn 2.5 in the limit 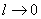 results in results in
|
and 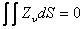 |
|
Similarly, eqn (2.6) simplifies to
|
and 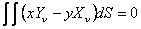 |
(2.8) |
Let's now see how these components of forces will change with change in orientation of the planes. In order to do that, let's consider the orthogonal rectilinear system
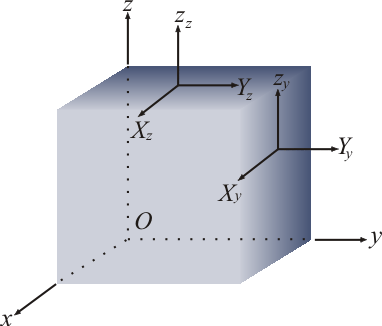
Figure 2.2
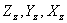 are the components of the stresses that act on the plane normal to the are the components of the stresses that act on the plane normal to the 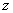 axis. While axis. While 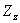 is the normal stress, is the normal stress, 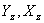 are the tangential or the shear stresses. Similarly are the tangential or the shear stresses. Similarly 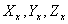 and and 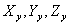 are the components of stresses acting on planes normal to the are the components of stresses acting on planes normal to the 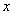 and and 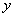 axes respectively. axes respectively.
Question is how these stresses are related to the components of stress on the plane normal to 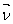 ? ? |