Solution of equations 19.7 and 19.8 along with boundary conditions 19.9 to 19.12 yield the following set of expressions for displacement of the film in 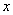 and and 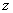 directions respectively directions respectively
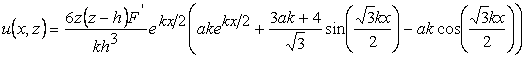 |
(19.13a) |
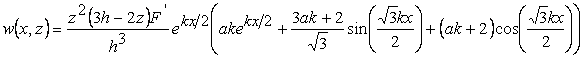 |
(19.13b) |
Where 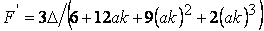 and and 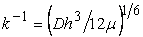 are two different characteristic length scales in the problem: the first accounts for the response of the plate to the displacement of its pivoted end, while the second length scale measures the relative deformability of the plate and the film in terms of the size of the effective contact zone. Thus the solutions of displacements are two different characteristic length scales in the problem: the first accounts for the response of the plate to the displacement of its pivoted end, while the second length scale measures the relative deformability of the plate and the film in terms of the size of the effective contact zone. Thus the solutions of displacements  and and  are obtained as oscillatory with exponentially decreasing amplitude away from the contact line. At are obtained as oscillatory with exponentially decreasing amplitude away from the contact line. At 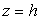 , the vertical displacement of the film and that of the contacting plate is expressed as: , the vertical displacement of the film and that of the contacting plate is expressed as:
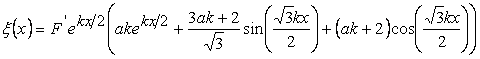 for for 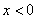 |
|
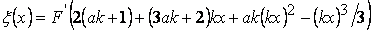 |
(19.14) |
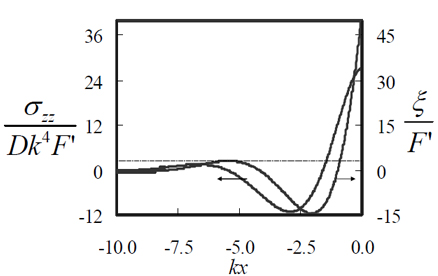
Figure 19.2 The normal stress in the film can be obtained as
 (19.15) (19.15)
The above figure shows the normal stress and vertical displacement in the film as a function of distance from the contact line. The wavelength of oscillation is found to be 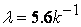 . .
|