Stress equilibrium relations and boundary conditions
The stress equilibrium relations for such a film in plane strain approximation is written in terms of the pressure field as,
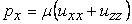 , , 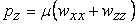 |
(19.1) |
Where, 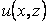 and and 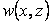 are the deformation components along are the deformation components along 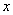 and and 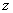 directions respectively and directions respectively and 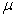 is the shear modulus of the adhesive material. We can use the plane strain approximation because the film is infinitely long along the is the shear modulus of the adhesive material. We can use the plane strain approximation because the film is infinitely long along the 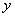 direction and the deformations remain independent of direction and the deformations remain independent of 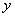 . The double derivatives of displacements represented by . The double derivatives of displacements represented by 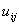 define the strain gradients. The incompressibility condition is written as define the strain gradients. The incompressibility condition is written as
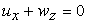 |
(19.2) |
These equations are solved using the following boundary conditions:
(a) Displacements along 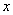 and and 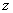 are zero at the film substrate interface: are zero at the film substrate interface:
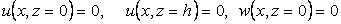 |
(19.3a) |
(b) The normal stress is continuous at the interface of the film and the plate, so that
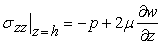 for for 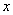 < 0 < 0 |
(19.3b) |
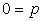 for for 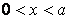 < 0 < 0 |
(19.3c) |
For small bending of plate in one dimension, the normal stress is equal to the bending stress which can be expressed in terms of the stiffness or flexural rigidity D of plate as
Here 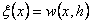 is the vertical displacement of the film at is the vertical displacement of the film at 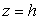 and and 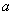 is the distance of the line of application of the peeling force from the contact line at is the distance of the line of application of the peeling force from the contact line at 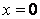 . .
We can simplify the above set of equations and boundary conditions because of large separation of characteristic length-scales along the 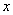 and and 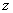 directions respectively , i.e. directions respectively , i.e. 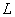 and and 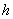 : : 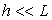 . .
For example, 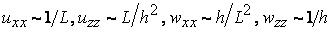 . Therefore, we can neglect all terms except . Therefore, we can neglect all terms except 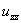 , so that the equations of equilibrium simplify to , so that the equations of equilibrium simplify to
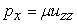 and and 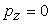 |
(19.4) |
|