Bending of a rod under concentrated vertical load
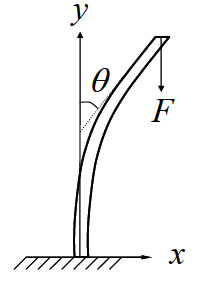
At any cross section, the internal stress is constant and is equal to 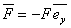 . Similar to earlier examples, the expression of the tangent to the rod at any location and its derivatives can be written in terms of the angle . Similar to earlier examples, the expression of the tangent to the rod at any location and its derivatives can be written in terms of the angle  , ,
 |
(14.9a,b) |
From equation (14.9)a and b,
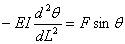 or or 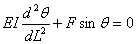 |
(14.10) |
Boundary conditions are:
At 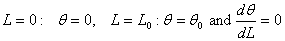 |
(14.11) |
Solution of equation 14.10:
Multiplying both left and write hand side of equation 14.10
Integrating,
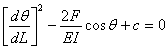 |
(14.12) |
Using boundary condition 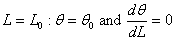 , we have, , we have,
From equation 14.12 we have,
 |
(14.13) |
Then, for small 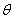 , we have , we have
 |
(14.14) |
The above expression yields a critical force for buckling of the rod under vertical load
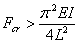 |
(14.15) |
|