Bending of a rod under concentrated load
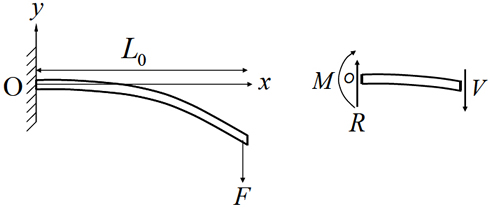
At the free end of the rod it is not acted upon by any reaction force. Say at any cross-section at a length 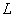 from wall, the reaction force is from wall, the reaction force is 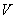 , then from force balance, , then from force balance,
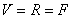 => => 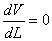 |
(14.1) |
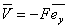 and and 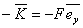 |
|
From equation 13.1, 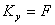 . Then from , . Then from , 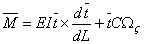 we have the following: we have the following:
For a circular rod 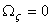 , so that , so that 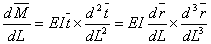 . .
But from equation 13.3, 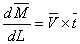 , so that , so that
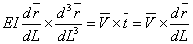 |
(14.2) |
Now from the following expression of the tangent to any point on the rod and its derivatives,
 |
(14.3a) |
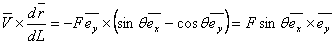 |
(14.3b) |
From equation 14.3a and b, we derive,
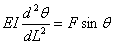 |
(14.4) |
Putting 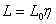 and and 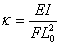 , we finally obtain, , we finally obtain,
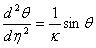 |
(14.5) |
Equation 8.36 is solved with the boundary conditions:
Integrating equation 14.5 and using b.c. 14.6,
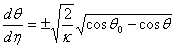 |
(14.7) |
Integrating the above expression we obtain the following integral, known as the elliptic integral
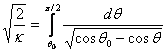 |
(14.8) |
and, 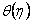 is obtained in terms of elliptic functions. is obtained in terms of elliptic functions.
The shape of the rod is finally obtained in terms of dimensionless lengths as: 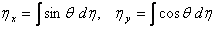
|