Affine Transformation (contd...)
Let 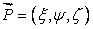 be the vector which transforms to a vector be the vector which transforms to a vector 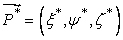 . .
If 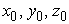 and and 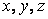 be the end points of vector be the end points of vector 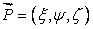 , then , then
Similarly
Where 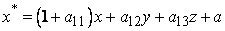 and and 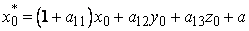 , etc. , etc.
Subtracting one obtains
It is easy to see that 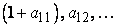 or in the short form or in the short form 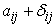 are components of a tensor and since are components of a tensor and since 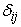 is a tensor, then is a tensor, then 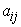 is a tensor. is a tensor.
Note that the components 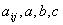 are constants. are constants.
From equation 1.7, we can conclude that two equal vectors remain equal after transformation and two parallel vectors remain parallel after transformation with the ratio of their lengths remaining unaltered due to the transformation.
Hence, it follows that two identical and identically oriented polygons remain identical and identically oriented after transformation. Since every geometric figure is some form of polygon, it follows that all parts of a body, independent of their deformations will deform in an identical manner. That is called homogeneous transformation.
|