Affine Transformation
The transformations of this form are called affine if the coordinates 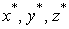 are linear functions of the coordinates are linear functions of the coordinates 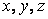
where 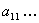 are constants. Above equations have nontrivial solution for are constants. Above equations have nontrivial solution for 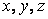 , so that the determinant , so that the determinant
Properties:
(a) Inverse affine transformation is also affine, because by solving 1.2 one obtains 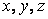 in terms of in terms of 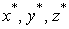 : :
(b) Points lying on a plane 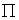 before transformation lies on a different plane before transformation lies on a different plane 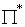 . .
Say 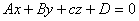 is the equation of plane is the equation of plane  , then after the transformation they lie on a different plane , then after the transformation they lie on a different plane 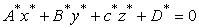 , which is the equation of plane , which is the equation of plane  . .
(c) Points lying on a straight line, which is the intersection of two different planes 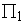 and and 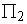 , will now lie again on a straight line, which is basically the intersection of two planes , will now lie again on a straight line, which is basically the intersection of two planes 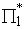 and and 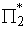 . Hence, any straight segment is transformed into a straight segment and any vector to a vector. . Hence, any straight segment is transformed into a straight segment and any vector to a vector.
|