Consider ‘n' number of independent variables for a physical option:
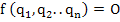
Or
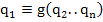
The theorem may be interpreted to state that one can form 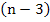 independent dimensionless groups of independent dimensionless groups of 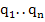 variables so that variables so that 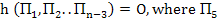 are the dimensionless groups, and M (mass), L (length) and T (time) are the primary dimensions used to describe the system. For some systems, angle are the dimensionless groups, and M (mass), L (length) and T (time) are the primary dimensions used to describe the system. For some systems, angle 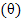 may also be taken as a primary group, for which one can have (n-4) independent dimensionless groups. We explain the utility of this method in the following examples: may also be taken as a primary group, for which one can have (n-4) independent dimensionless groups. We explain the utility of this method in the following examples:
- Reconsider the previous example of drag on a sphere immersed in a flowing fluid. From the physics of the problem, the independent variables that govern the drag are identified as
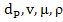 . Therefore, . Therefore,
|