In many engineering applications, scale-up or scale-down of a chemical process or equipment is frequently required. It is not practical to conduct experiments for all conditions of a process to predict the data. The dimensional analysis is a commonly employed technique to scale-up or down a process, and also, predict the results for different conditions.
As an example, consider drag on a sphere falling in stagnant water. If Reynolds number based on the particle size is less than 1, drag can be theoretically calculated as 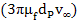
Alternatively, we can write a general symbolic equation based on our experience:
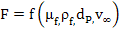 . A few experiments may also be conducted to gain insight into numerical values for F. It is easy to show that . A few experiments may also be conducted to gain insight into numerical values for F. It is easy to show that 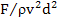 is a dimensionless quantity, which can be interpreted as the force per unit kinetic energy per unit cross-sectional area. Realizing that Reynolds number has a mechanistic role to play on the drag, one can write is a dimensionless quantity, which can be interpreted as the force per unit kinetic energy per unit cross-sectional area. Realizing that Reynolds number has a mechanistic role to play on the drag, one can write
|