There are many different possible choices of atomic orbitals (the basis set). The Slater Type Orbitals [Slater 1930] (STO’s) have the following form in Cartesian coordinates:
(1.18) |
The Gaussian Type Orbitals [Boys 1950] (GTO’s) have the following form in Cartesian coordinates:
(1.19) |
N is the normalization constant; a, b, c are non-negative integers which control the angular momentum L = a + b + c. When a+b+c = 0 (that is, a = 0, b = 0, c = 0), the Gaussian is called an s-type Gaussian; when a+b+c = 1, we have a p-type Gaussian, which contains the factor x, y or z. ς controls the width of the orbital – large ς gives tight function and small ς gives diffuse function.. Almost all modern ab-initio calculations employ Gaussian Type Orbital (GTO) basis sets. These bases, in which each atomic orbital is made up of a number of Gaussian probability functions, have considerable advantages over other types of basis sets for the evaluation of one- and two-electron integrals. They are much faster computationally than, for instance, equivalent Slater orbitals. The Gaussian series of programs deals exclusively with Gaussian type orbitals and includes several optional GTO basis sets of varying size. This is one of the main advantages of such a widely distributed program system - the methods and basis sets used become standard and a direct comparison with literature data is often possible.
The simplest of the optional basis sets in Gaussian03 [Frisch et al., 2004] is the STO-3G [Hehre et al 1969, Collins et al 1976]. STO-3G is an abbreviation for Slater-Type-Orbitals simulated by 3 Gaussian functions each. This means that each atomic orbital consists of 3 Gaussian functions added together. The coefficients of the Gaussian functions are selected so as to give as good a fit as possible to the corresponding Slater-type orbitals. STO-3G is a minimal basis set. This means that it has only as many orbitals as necessary to accommodate the electrons of the neutral atom. Because a complete basis set of p-orbitals must be added to maintain spherical symmetry, the elements boron to neon each have five atomic orbitals: 1s, 2s, 2px, 2py, and 2pz; for beryllium and lithium a minimal basis set actually requires only 1s and 2s orbitals. In STO-3G, however, the three 2p-orbitals are also included for these elements in order to give a consistent description across the periodic table. Because there is only one best fit to a given type of Slater orbital (1s, 2p, etc.) for each number of Gaussian functions, all STO-3G basis sets for any row of the periodic table are identical except for the exponents ς of the Gaussian functions. These are expressed as a scale factor, the square of which is used to multiply all exponents in the original best-fit Gaussian functions. In this way the ratios of the exponents of the individual Gaussians to each other remain constant, but the effective exponent of the entire orbital can be varied. The exponents, or scale factors, can be considered to be a measure of the extent of the orbital. A low exponent indicates a diffuse (and therefore relatively high energy) orbital; high exponents indicate compact orbitals close to the nucleus.
The STO-3G basis set is very economical, having only one basis function (or atomic orbital) per hydrogen as atom (the 1s), five per atom from Li to Ne (1s, 2s, 2px, 2py, and 2pz) and nine per atom for the second-row elements Na to Ar (1s, 2s, 2px, 2py, 2pz, 3s, 3px, 3py, and 3pz). Although STO-3G remained a standard basis set for ab-initio optimizations for several years, it has eventually been replaced by small split-valence basis sets and is now hardly used. Its weaknesses proved to be - overestimation of the stability of small rings; overemphasis of the π-acceptor characteristics of electropositive elements of the first row; and total failure for the second-row electropositive elements, especially sodium.
The greatest problem of any minimal basis set is its inability to expand or contract its orbitals to fit the molecular environment. One solution to the problem is to use either split-valence or double zeta basis sets. In these bases the atomic orbitals are split into two parts – a compact inner orbital and a more diffused outer orbital. The coefficients of these two types of orbitals can be varied independently during the molecular orbitals construction in the self consistent field SCF procedure. Thus the size of the atomic orbital that contributes to the molecular orbital can be varied within the limits set by the inner and outer basis functions (Fig. 2.1). Split-valence basis sets split only the valence orbitals in this way; whereas double zeta bases also have split core orbitals (double zeta implies two different exponents). The split –valence basis set most widely used for the early calculations was 4-31G [Ditchfield et al 1971.,Hehre et al .,1972, Hariharan and Pople,1974, Gordon et al., 1982]. This nomenclature means that the core orbitals consist of 4 Gaussian functions; inner valence orbitals have 3 Gaussian functions; and outer valence orbitals have 1 Gaussian function.
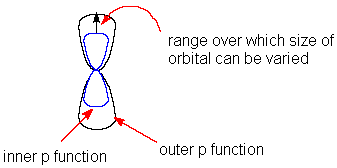
Figure 1.2 Split-valence p-orbital