1.2 One electron atoms

In an atom that contains a single electron, the potential energy depends upon the distance between the electron and the nucleus as given by the Coulomb equation. The Hamiltonian thus takes the following form:

(1.7)

In atomic units this takes the form

(1.8)

For the hydrogen atom, the nuclear charge, Z, equals +1. r is the distance of the electron from  the nucleus. The helium cation, He⁺, is also a one-electron atom but has a nuclear charge of  +2. As atoms have spherical symmetry it is more convenient to transform the Schrodinger  equation to polar coordinates r, θ  and Φ, where r is the distance from the nucleus (located at  the origin), θ is the angle to the z axis and Φ is the angle from the x axis in the xy plane  (See figure 1.1 below). The solutions can be written as the product of a radial function R(r), which  depends only on r, and an angular function Y(θ,Φ) called a spherical harmonic, which that depends on θ  and Φ.

(1.9)

The wavefunctions are commonly referred to as orbitals and are characterised by three quantum numbers n, m and l. The quantum numbers can adopt values as follows:
n: principal quantum number: 0,1, 2,...
l: azimuthal quantum number: 0,1, ... (n - 1)
m: magnetic quantum number: —l, — (l — 1),... 0... (l — 1), l.

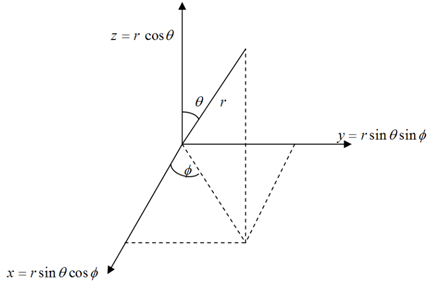
  Figure 1.1: Relationship between spherical polar and Cartesian coordinates
(Adapted from Leach,2001)