4.3.2 Laminar flow
Hausen presents the following empirical relations for fully developed laminar flow in tubes at constant wall temperature.
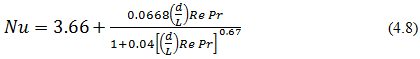
The heat transfer coefficient calculated from eq. 4.8 is the average value over the entire length (including entrance length) of tube 
.
Sieder and Tate suggested a simple relation for laminar heat transfer in tubes.
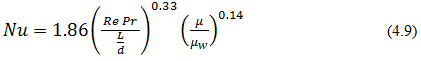
The condition for applicability of eq. 4.9:
where, μ is the viscosity of the fluid at the bulk temperature and μw is that at the wall temperature Tw . The other fluid properties are at mean bulk temperature of the fluid. Here also the heat transfer coefficient calculated from eq. 4.9 is the average value over the entire length (including entrance length) of tube .
The empirical relations shown in eq. 4.2-4.9 are for smooth pipe. However, it case of rough pipes, it is sometimes appropriate that the Reynolds analogy between fluid friction and heat transfer be used to effect a solution under these conditions and can be expressed in terms of Stanton number.
In order to account the variation of the thermal properties of different fluids the following equations may be used (i.e. Stanton number multiplied by 
),
where,
is the mean free velocity. The friction factor can be evaluated from Moody’s chart.