Let us calculate the wavelength of the electrons that are accelerated by a potential of 10 kV. Substituting the value of V (10,000 V) in equation 17.6 gives:
![]()
The wavelength of the electrons accelerated under 10 kV potential is therefore smaller than all the atoms. In practice, acceleration voltages up to 1000 kV are used in analytical electron microscopes therefore achieving the wavelengths below 1 pm.
Resolution
Unlike light microscopy, electron microscopy demands very high vacuum (Pressure ~10-5 Pa or less). This is due to very high scattering of electrons by the molecules present in the air. An electron microscope may require a mean free path of ~1-2 m, therefore a very high vacuum. In electron microscope, magnetic fields act as the lenses to focus the electron beams. The electrons therefore do not experience any significant change in refractive index as they pass through the lenses. Under high vacuum, the refractive index in an electron microscope therefore can be assumed to be unity ( n ≈ 1). Furthermore, the electrons are deflected by very small angles, therefore, sinα ≈ α . The equation for resolution (equation 14.1) therefore gets reduced to:
![]() ......................................................... (14.2)
......................................................... (14.2)
Assuming α = 5 degrees (0.1 radian), the theoretical resolution of an electron microscope operating at a reasonable accelerating voltage of 100 kV (λ = 3.7 pm; try calculating yourself using equation 17.6) turns out to be 2.26 pm. An electron microscope should therefore be able to resolve all the atoms. In practice, however, resolutions better than 0.2 nm are rarely achieved largely due to the lens aberrations.
Electron sources and lenses
Of the various methods of generating electrons, two are more frequently used in the electron guns used for electron microscopy: thermionic electron emission and field emission . Most electron microscopes use thermionic emission of electrons from a heated filament. Being one of the cheapest and simplest thermionic sources, tungsten is most widely used in thermionic electron guns. Figure 17.1A shows a diagrammatic representation of a tungsten filament electron gun. The filament is placed in a cylindrical case called a Wehnelt cylinder or Wehnelt cap. Wehnelt cap has an aperture and the filament is situated immediately above the aperture. Below the Wehnelt cap lays an anode that causes the emitted electron to accelerate. A negative potential is applied to the Wehnelt cap that focuses the electrons emitted by the filament into a narrow beam. An electron gun therefore acts both as an electron source as well as a lens. The brightness of the electron beam is defined as the current density per unit solid angle. Tungsten filament provides a brightness of ~109 A·m-2·sr-1 . Further ten-fold increase in brightness can be achieved using lanthanum hexaboride (LaB6) instead of tungsten filament.
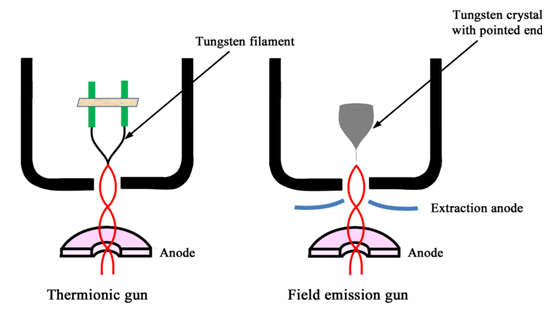
Figure 17.1 Electron guns: A tungsten filament Wehnelt thermionic gun (A) and field emission gun (B)