Let us assume that, the unprimed and primed coordinate systems are as shown in Figure 2.2. The transformation matrix for this rotation is given in Equation (2.1). Then, the components 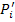 can be given as can be given as
Note: In two dimensional case, the above transformation is written as
Equation (2.3) can also be written in an inverted form to give the components Pi in unrotated axes in terms of components 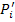 in rotated axes system as in rotated axes system as
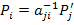 |
(2.5) |
The rotation matrix aij in Equation (2.2) has a property that
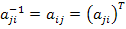 |
(2.6) |
Now, we will extend the concept to transform a second order tensor. Let us transform the stress tensor 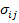 as follows as follows
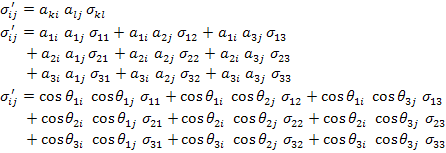 |
(2.7) |
The transformation of a fourth order tensor 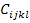 is given as is given as
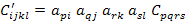 |
(2.8) |
The readers are suggested to write the final form of Equation (2.8) using similar procedure used to get the last of Equation (2.7). |