In this lecture, we are going to introduce some concepts from solid mechanics which will be useful for better understanding of this course. It is presumed that the readers have some basic knowledge of linear algebra and solid mechanics.
In solid mechanics, each phase of a material is considered to be continuum, that is, there is no discontinuity in the material. Thus, in this course individual fibres and the matrix of a lamina/composite are considered to be continuum. Further, this results in saying that heterogeneous composite is also a continuum.
In this lecture, we will introduce some of the notations that will be followed for the rest of the course. Hence, the readers are advised to understand them clearly before they proceed to further lectures.
Concept of Tensors
Tensors are physical entities whose components are the coefficients of a linear relationship between vectors.
The list of some of the tensors used in this course is given in Table 2.1.
Table 2.1 List of some of the tensor quantities
|
Quantity |
Live subscripts |
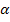
|
Scalar (zeroth order tensor) |
0 |
vi |
Vector (first order tensor) |
1 |
σij,εij |
Second order tensor |
2 |
Cijkl |
Fourth order tensor |
4 |
It is often needed to transform a tensorial quantity from one coordinate system to another coordinate system. This transformation of a tensor is done using direction cosines of the angle measured from initial coordinate system to final coordinate system. Let us use axes 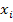 as the initial coordinate axes and as the initial coordinate axes and 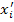 as the final coordinate axes (denoted here by symbol prime – as the final coordinate axes (denoted here by symbol prime –  ). Now, we need to find the direction cosines (denoted here by aij) for this transformation relation. Let us use the convention for direction cosines that the first subscript (that is, i) of aij corresponds to the initial axes and the second subscript (that is, j) corresponds to final axes. The direction cosine correspondence with this convention in 3D Cartesian coordinate system is given in Table 2.2. The corresponding Cartesian coordinate systems are shown in Figure 2.1. ). Now, we need to find the direction cosines (denoted here by aij) for this transformation relation. Let us use the convention for direction cosines that the first subscript (that is, i) of aij corresponds to the initial axes and the second subscript (that is, j) corresponds to final axes. The direction cosine correspondence with this convention in 3D Cartesian coordinate system is given in Table 2.2. The corresponding Cartesian coordinate systems are shown in Figure 2.1.
Table 2.2 Direction cosines for 3D Cartesian coordinate system
Figure 2.1 Rectangular or Cartesian coordinate systems |
|