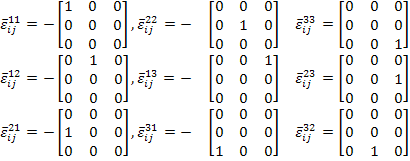 |
(7.142) |
Due to symmetry considerations one needs to consider only the first six strains components in the linear combination. Substituting these unit strains in right hand side of Equation (7.141) we get the stress tensor
Now, putting this stress tensor in Equation (7.141) we solve the resulting auxilliary problem as
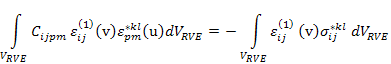 |
(7.143) |
The periodicity of the strain field 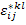 is obtained by constraining equal displacements on opposite sides of RVE. Once is obtained by constraining equal displacements on opposite sides of RVE. Once 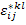 is determined, the solution to Equation (7.141) is obtained by is determined, the solution to Equation (7.141) is obtained by
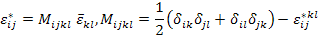 |
(7.144) |
where 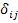 is Kronecker delta and is Kronecker delta and 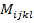 is the local structure tensor. When the relationship between local RVE strain and the average strain is substituted into the macroscopic equilibrium equations, we get is the local structure tensor. When the relationship between local RVE strain and the average strain is substituted into the macroscopic equilibrium equations, we get
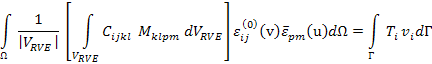 |
(7.145) |
Here, it should be noted that the terms 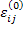 and and 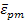 are outside the integration over the RVE as they represent the average strain, which is constant, over RVE. The homogenization approach gives the equivalent properties of the composite laminate. The effective stiffness tensor, are outside the integration over the RVE as they represent the average strain, which is constant, over RVE. The homogenization approach gives the equivalent properties of the composite laminate. The effective stiffness tensor, 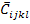 is defined (as in standard mechanics approach in Equation (7.98)) is defined (as in standard mechanics approach in Equation (7.98))
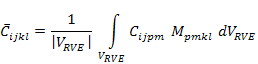 |
(7.146) |
Using this effective stiffness tensor, the final form of macroscopic equilibrium equation may be written as
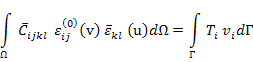 |
(7.147) |
It is important to note that the effective stiffness tensor obtained from Equation (7.146) is independent of size of RVE due to periodicity assumption used in obtaining 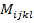 . .
Note: The effective stiffness tensor obtained using homogenization approach is independent of size of RVE as periodicity assumption has been imposed on RVE. In case of standard mechanics such boundary conditions are not imposed. Hence, the effective stiffness obtained is dependent on the size of RVE. This fact can be explained by St. Venant’s principle for applied displacement or traction boundary conditions. However, when St. Venant effect is not significant (as in case of analysis with multi cell RVE) the two approaches may yield the same results.
|