Thus, using this definition the phase averaged strains in fibre and matrix can be written using Equation. (7.109) and Equation (7.110) as

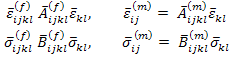(7.112)

Now, using the first of Equation (7.112) in Equation (7.107) composite average stress is given as

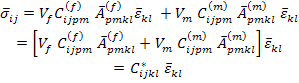(7.113)

Similarly, using the second of Equation (7.112) in Equation (7.108) composite average strain is given as

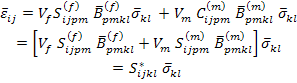(7.114)

Equation (7.102) can be written using the second of Equation (7.112) as

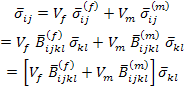(7.115)

It should be noted that in above equation the stresses on left and right hand side are the composite average stresses. Hence, they are same. Thus, the bracketed term in above equation is an identity tensor of fourth order, that is,

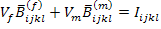(7.116)

Likewise, from Equation (7.104) and the first of Equation (7.112) we can write

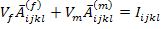(7.117)

Now using the Eq. (7.117) in Eq. (7.113), we can write

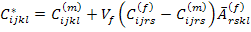(7.118)

Similarly, using Equation (7.116) in Equation (7.114), we can write

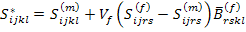(7.119)