In the above derivation it is assumed that the material behaviour is same everywhere for fibre and matrix. Further, Equation (7.103) has been used in above equation. The above equation can be written in terms of compliance of fibre and matrix material as
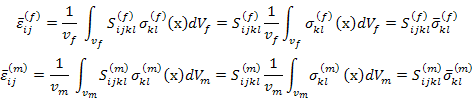 |
(7.106) |
Using Equation (7.105) in Equation (7.102) we get the average stress in composite in terms of volume fractions, stiffness tensor and phase averaged strains as
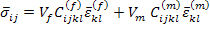 |
(7.107) |
Similarly, the average composite strain in terms of phase averaged stresses in the fiber and matrix, respective compliances and volume fractions using Equation (7.106) in Equation (7.104) is given as
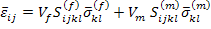 |
(7.108) |
Note: It can be shown that if an RVE is subjected to homogeneous traction on its boundary, that is,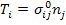 with with 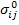 is a constant state of stress, then the average stress in composite is is a constant state of stress, then the average stress in composite is
Similarly, if an RVE is subjected to homogeneous displacement on its boundary, that is, 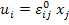 with with 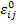 is a constant strain, then the average strain in the composite is is a constant strain, then the average strain in the composite is
The local structure tensor used in Equation (7.94) in standard mechanics approach to define the local strains in terms of composite average strains. Hill [4] used this concept to relate the pointwise stresses and strains in fibre and matrix with average stresses and strains in composite through pointwise phase concentration factors. The pointwise strains in fibre and matrix are given as
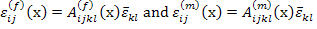 |
(7.109) |
where 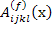 and and 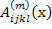 are the pointwise fibre and matrix strain concentration factors, respectively. Similarly, the pointwise stresses in fibre and matrix are given as are the pointwise fibre and matrix strain concentration factors, respectively. Similarly, the pointwise stresses in fibre and matrix are given as
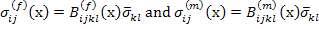 |
(7.110) |
where 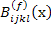 and and 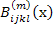 are the pointwise fibre and matrix stress concentration factors, respectively. are the pointwise fibre and matrix stress concentration factors, respectively.
The local strains and stresses in fibre and matrix as given in Equation (7.109) and Equation (7.110) can be integrated over their respective volumes to give the phase averaged strains and stresses in terms of phase averaged concentration factors 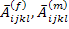 and and 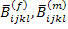 . The phase averaged concentration factors as defined are given below. . The phase averaged concentration factors as defined are given below.
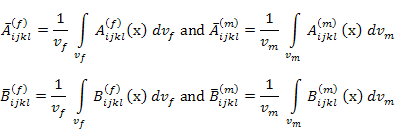 |
(7.111) |
|