Effective Axial (Major) Poison’s Ratio 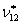 : :
To determine the effective axial Poisson’s ratio we consider the loading as in the case applied for determining the effective axial modulus. Here, for this loading we have 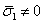 and other stresses are zero. We define the effective axial Poisson’s ratio as and other stresses are zero. We define the effective axial Poisson’s ratio as
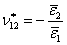 |
(7.22) |
The effective strain in direction 2 from Figure 7.3(b) and (c) can be given as
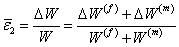 |
(7.23) |
Now, the changes in 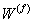 and and 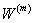 can be obtained using the Poisson’s ratio of individual constituents. The axial Poisson’s ratios for fibre and matrix are given as can be obtained using the Poisson’s ratio of individual constituents. The axial Poisson’s ratios for fibre and matrix are given as
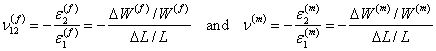 |
(7.24) |
Thus, the changes in 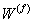 and and 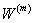 are given as are given as
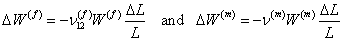 |
(7.25) |
The total change in 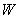 is given as is given as
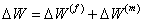 |
(7.26) |
The strain in direction 2 for the composite can be given using Equation (7.25) and Equation (7.26) as
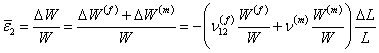 |
(7.27) |
Here, 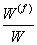 and and 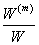 denote the fibre and matrix volume fractions for same length of fibre and matrix. Note that denote the fibre and matrix volume fractions for same length of fibre and matrix. Note that 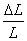 denotes the effective axial strain denotes the effective axial strain 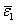 . Thus, from Eq. (7.27) the effective axial Poisson’s ratio is written as . Thus, from Eq. (7.27) the effective axial Poisson’s ratio is written as
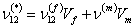 |
(7.28) |
The above equation is the rule of mixtures expression for composite axial Poisson’s ratio.
|