Effective Transverse Modulus 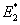 : :
Here, we are going to derive the effective transverse modulus by loading the RVE in direction 2 as shown in Figure 7.4(a). There are two considerations while deriving this effective modulus. The first approach considers that the deformation of the each constituent is independent of each other as shown in Figure 7.4(b) and (c) and the deformation in direction 1 is not considered. The second approach considers that deformations of the fibre and matrix in direction 1 are identical as they are perfectly bonded.
To calculate the effective modulus in direction 2, a stress 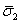 is applied to the RVE as shown in Figure 7.4(a). is applied to the RVE as shown in Figure 7.4(a).
First Approach:
As mentioned, the fibre and matrix deform independently of each other. The resulting deformation in direction 1 is not considered here. This assumption is simplistic and was used by early researchers.
The fibre and matrix are subjected to same state of stress. The state of stress is unidirectional, that is, 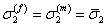 . Now, using the individual moduli and deformations in direction 2, these stresses can be given as . Now, using the individual moduli and deformations in direction 2, these stresses can be given as
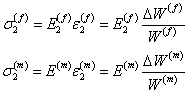 |
(7.29) |
From this equation we can write the individual deformations, which give the total deformation in direction 2 as
 |
(7.30) |
Now, the composite strain in direction 2 can be calculated from the definition as
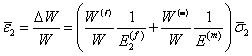 |
(7.31) |
Figure 7.4: (a) Undeformed unit cell under uniform  stress (b) and (c) deformed individual constituents of the unit cell stress (b) and (c) deformed individual constituents of the unit cell |
Introducing the volume fractions in the above equation,
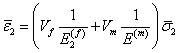 |
(7.32) |
Noting that 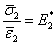 , from the above equation, we get , from the above equation, we get
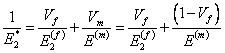 |
(7.33) |
This equation is the rule of mixtures equation for effective modulus 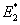 . .
|