Laminate Coefficient of Thermal Expansion
The derivation of laminate coefficients of thermal expansion is dealt here for symmetric laminates. This is because there is no extension-bending coupling due to the fact that for symmetric laminates 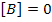 . .
Let us derive the expression for the coefficient of thermal expansion for laminate. Let us define the coefficient of thermal expansion for laminate, 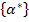 , as the laminate mid-plane strain, , as the laminate mid-plane strain, 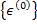 , to the per unit uniform change in temperature, , to the per unit uniform change in temperature, 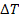 . Thus, . Thus,
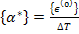 |
(5.106) |
Now for symmetric laminates with pure thermal loading, we have
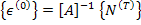 |
(5.107) |
Combining Equation (5.105) and Equation (5.106), we get
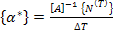 |
(5.108) |
For a uniform temperature change the equivalent thermal force is given as
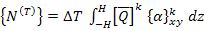 |
(5.109) |
Thus, the laminate coefficient of thermal expansion becomes
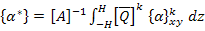 |
(5.110) |
It is known that the 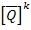 and and 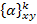 are constant in each lamina in thickness direction. Thus, the integration over thickness can be simplified as the summation over laminae thicknesses as are constant in each lamina in thickness direction. Thus, the integration over thickness can be simplified as the summation over laminae thicknesses as
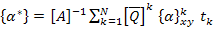 |
(5.111) |
where, 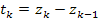 is the thickness of kth lamina. is the thickness of kth lamina.
Figure 5.12 shows the variation of 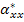 for for 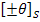 laminate along with laminate along with 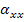 of layer for of layer for 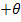 for AS4/3501-6 Epoxy material from Soden et al [4]. Similarly, Figure 5.13 and Figure 5.14 show the variation of for AS4/3501-6 Epoxy material from Soden et al [4]. Similarly, Figure 5.13 and Figure 5.14 show the variation of 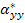 and and 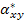 . .
From these figures it is seen that these coefficients vary from positive to negative values. Further, it is observed that the coefficient of thermal expansion depends upon stacking sequence. This fact is very important from laminate designing point of view where it is used in an environment with large thermal gradient. One can choose a laminate sequence for which a coefficient of thermal expansion is zero.
From Equation (5.109) and Equation (5.110) for a uniform temperature change, the equivalent thermal force is written as
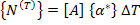 |
(5.112) |
|