Laminate Theory with Thermal Effects:
In the classical laminate theory we make the assumption that the total strain is superposition of mechanical strain and thermal strains. Thus,
 |
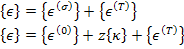(5.96) |
where, 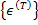 is the thermal strain in laminate. We can write the stresses in global direction for laminate as
Thus, using Equation (5.95) in above equation, we get
 |
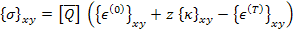(5.97) |
Now we find the resultant in-plane forces as
Recalling the development of classical laminate theory with the use of Equation (5.21), we write
 |
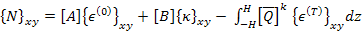(5.98) |
Let us define
 |
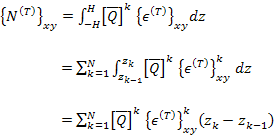(5.99) |
as the effective laminate thermal forces per unit length. Thus, with this definition we can write Equation (5.97) as
 |
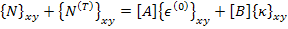(5.100) |
Now let us define the resultant moments using Equation (5.96) as
With the use of Equation (5.21) and Equation (5.27), we write
 |
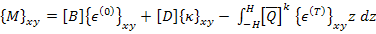(5.101) |
Let us define
 |
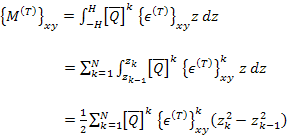(5.102) |
as the effective laminate thermal moments per unit length. Thus, with this definition we can write Equation (5.101) as
 |
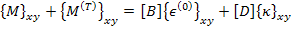(5.103) |
Combining Equation (5.99) and Equation (5.102), we write
 |
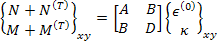(5.104) |
The inverse of this equation is written as
 |
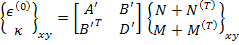(5.105) |
| 
