Introduction:
In the previous lecture we have introduced the laminate theory. In this lecture we are going to develop laminate constitute equations for classical laminate theory. In the previous lecture we have introduced the in-plane stress resultants and resultant moments. These resultant quantities will be related to mid-plane strains and curvatures. Further, we will introduce classification of laminates.
Laminate Constitutive Relations:
Using Equations (5.18) and (5.24) we can write a combined equation as
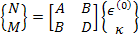 |
(5.28) |
This equation is the fundamental equation in classical laminate theory and is known as constitutive equation. This equation can be written in expanded form as
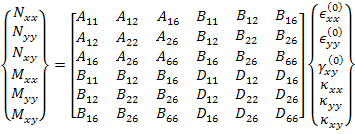 |
(5.29) |
It should be noted that the matrices A, B and D are symmetric. Hence, the matrix in above equation is also a symmetric matrix. The inverse constitutive relations of Equation (5.28) can be written as
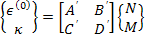 |
(5.30) |
The matrix 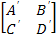 is obtained by using individual relations for is obtained by using individual relations for 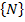 and and 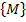 as follows. We write for as follows. We write for 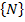 and and 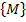 as as
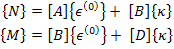 |
(5.31) |
From the first of the above equation we can write
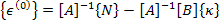 |
(5.32) |
Putting this in second of Equation (5.31) we get
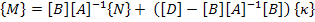 |
(5.33) |
|