Moisture Effect:
The hygroscopic expansion in principal material direction is proportional to the amount of percentage weight of moisture absorbed. Further, the hygroscopic expansion will be in principal normal directions only. This expansion will not lead to any shear. Thus, we write the hygral strains in principal directions for planar problem as
 |
(4.54) |
Here, 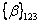 denotes the coefficient of hygroscopic expansion in principal material directions for planar problem and denotes the coefficient of hygroscopic expansion in principal material directions for planar problem and 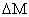 denotes the amount by percentage weight of moisture absorbed. denotes the amount by percentage weight of moisture absorbed.
Now let us transform the hygroscopic strains in global coordinate system as
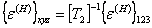 |
(4.55) |
Using Equation (4.54), we can write
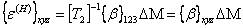 |
(4.56) |
where
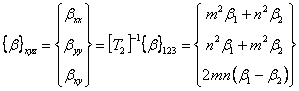 |
(4.57) |
It is clearly seen from Equation (4.48) and Equation (4.57) that 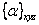 and and 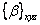 behave in a similar way. behave in a similar way.
Hygro-Thermo-Elastic Constitutive Equations:
When hygral and thermal effects are present along with mechanical strains, then the total strain in principal material direction is given as
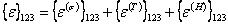 |
(4.58) |
Using Hooke’s low for mechanical strain and solving for stress the hygro-thermal constitutive equation, we get
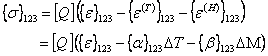 |
(4.59) |
Equation (4.59) can be written to give stresses in global directions as
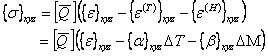 |
(4.60) |
where 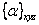 and and 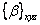 are as given in Equation (4.48) and Equation (4.57), respectively. are as given in Equation (4.48) and Equation (4.57), respectively.
|