Homework:

1. Write the number of independent elastic constants for 3D hyperelastic, monoclinic, orthotropic, transversely isotropic and isotropic materials.
   
   
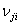2. Are the Poisson’s ratio  and  independent of each other for an orthotropic unidirectional lamina?
   
   
3. Take the form of stiffness matrix for an orthotropic material as given in Equation (3.26). Using any symbolic calculation software like Maple or Mathematica, obtain the inverse of this matrix and confirm that the form of compliance matrix written in Equation (3.42) is correct. Further, confirm that this matrix is symmetric. (One should be able to do this using the concepts of linear algebra alone.)
   
   
4. Extend the Problem 3 to get the stiffness matrix given in Equation (3.51).