:

The stress transformations for this coordinate transformations are (from the first of Equation (3.12) and Equation (3.29))

The same can be seen from the stresses shown on the same cube in x₁, x₂, x₃ and 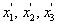 coordinate systems in Figure 3.6 (a) and (b), respectively. The comparison of the stress terms leads to the stiffness matrix as given in Equation (3.26).

Note: It is clear that if any two orthogonal planes are planes of material symmetry the third mutually orthogonal plane has to be plane to material symmetry. We have got the same stiffness matrix when we considered two sets of orthogonal planes. Further, if we proceed in this way considering three mutually orthogonal planes of symmetry then it is not difficult to see that the stiffness matrix remains the same as in Equation (3.26).