At equilibrium state, the force balance on bob can be written by the following expression;

(7.3.2)

By definition, all these forces terms can be expressed in the following form;

(7.3.3)

where, is the total volume of the bob, is the frontal area of the bob, is the mean flow velocity in the annular space between the bob and tube, is the drag coefficient, g is the acceleration due to gravity, are the fluid density and float density, respectively. Both Eqs (7.3.2 &7.3.3) can be combined to obtain the expression for and subsequently volume flow rate .

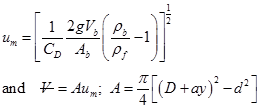(7.3.4)

Here, A is the annular area, is the diameter of the tube at inlet, d is the maximum bob diameter, y is the vertical distance from the entrance and a is the constant indicating the tube taper. Since the drag coefficient depends on the Reynolds number and fluid viscosity, special bob may be used to have constant drag coefficient. It is also possible to decide appropriate geometrical dimensions so that a linear relation is obtained for the expression given by the Eq. (7.3.4).

(7.3.5)

Since the response of rotameter is linear, its resolution is same for both higher and lower flow rates. The accuracy for these types of devices is typically ±5%. However, rotameters have certain drawbacks such as vertical installation and inability for measurements of opaque fluids because the float may not be visible.

Thermal Anemometers

The thermal anemometers are often used in research applications to study rapidly varying flow conditions. When, a heated object is placed in a flowing fluid, it tends to lose heat to the fluid. The rate, at which the heat is lost, is proportional to the flow velocity. If the object is heated to a known power and placed in the flowing fluid, then heat will be lost to the fluid. Eventually, the object will reach to a temperature which is decided by the rate of cooling. However, if the temperature of the object is to be maintained constant, then the input power needs to be changed which is proportional to the fluid velocity. So, the heating power becomes a measure of velocity. The concept of using thermal effects to measure the flow velocity was introduced in late 1950s. The thermal anemometers have extremely small sensors and are useful to measure instantaneous velocity at any point in the flow without disturbing the flow appreciably (Fig. 7.3.2).

 

 

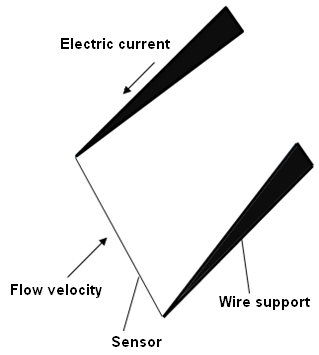
Fig. 7.3.2: Operating principle of a thermal anemometer.

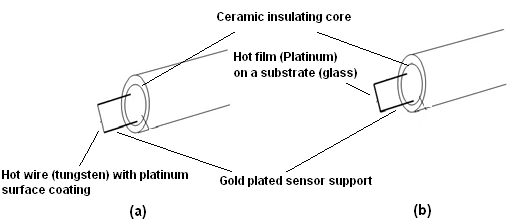
Fig. 7.3.3: A hot-wire/hot film thermal anemometer with its support system:

(a) hotwire; (b) hot-film.