Step V: Now, first pi term is formed between the dependent variable and the repeating variables. It is written as,

(6.1.5)

Since, this combination need to be dimensionless, it follows that

(6.1.6)

The exponents must be determined by equating the exponents for each of the terms i.e.

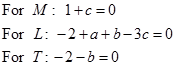(6.1.7)

The solution of this algebraic equations gives . Therefore,

(6.1.8)

The process is repeated for remaining non-repeating variables with other additional variable so that,

(6.1.9)

Since, this combination need to be dimensionless, it follows that

(6.1.10)

Equating the exponents,

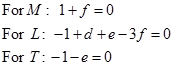(6.1.11)

The solution of this algebraic equation gives . Therefore,

(6.1.12)

Step VI: Now, the correct numbers of pi term s are formed as determined in “Step III”. In order to make sure about the dimensionality of pi terms , they are written as,

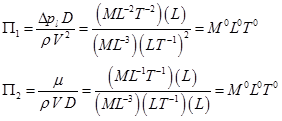(6.1.13)

Step VII: Finally, the result of dimensional analysis is expressed among the pi term s as,

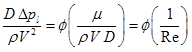(6.1.14)

It may be noted here that Re is the Reynolds number.

 

Remarks

- If the difference in the number of variables for a given problem and number of reference dimensions is equal to unity, then only one Pi term is required to describe the phenomena. Here, the functional relationship for the one Pi term is a constant quantity and it is determined from the experiment.

(6.1.15)

- The problems involving two Pi terms can be described such that

(6.1.16)

Here, the functional relationship among the variables can then be determined by varying and measuring the corresponding values of .